お久しぶりです!5月3日に任地を離れ、スワコップムントという街で開催されていたNational Mathematics Congress というイベントに参加してきました。ナミビア各地から算数・数学に関わる教員が集まる、研修会のようなものです。5月11日にようやく任地に帰ってきました。なかなかの長旅だったけれど、得られたものもたくさんありました。
コングレスでは、ただ単に算数・数学を教えるのではなく、数学的感覚を養おうということが繰り返し言われていました。
しょっぱなから批判まじりで良くないとは思うけれど、今日の裏タイトルは「違和感」こちらの人たちの感覚に少し触れつつ、共感はできないながらも…自分なりに色々と考えたことを書きたいと思います。
13−8、どうやりますか?
・13-8=5 で、13を10と3に分けて、10から8を引いて2、2と3で5 はナンセンス。という話がありました。その時、会場からも笑いが起きていて、こういう考え方よりも、9,10,11,12,13ってカウントアップした方がいいって言っていました。
引き算なのにカウントアップなんだ、ってところがツッコミどころ…それなら8を3と5に分けて、13-3=10、10-5=5ってするか、カウントダウンした方がよほど引き算の感覚を育てられるんじゃないのかなって思うな。
14+29、一の位から考えますか?
・14+29=43 で、一のくらいからでなく十の位から計算することを勧めていました。これも数的感覚を育てるためなんだって。10+20=30、4+9=13、30と13で43。こちらで言うexpanded notation のこと。
その考えは分かるんだけど、大きい数になれば筆算の方が圧倒的に速くて正確だと思う。位が違う数だったら間違えやすいし、二通りのやり方を切り替えるのも混乱する…概念理解と技能の向上は分けて考えるべきだと思う。
Sense making って言葉を何度も聞いたけれど、すでに持ってるセンスを使ってる感じだった。そのセンスを育てるのにはどうしたらいいかって言うのをもっと聞きたかったし、数の感覚、図形の感覚、図で考える感覚などあるわけだから、もっともっと掘り下げていきたいって思った。
分配法則の教え方
・分配法則で謎の表を書いていたこと
これは!分配法則を面積で考えるこの表。概念理解に役立ったって話がありました。+と-をかけると-になるわけだし、面積は有効なのかなぁ…
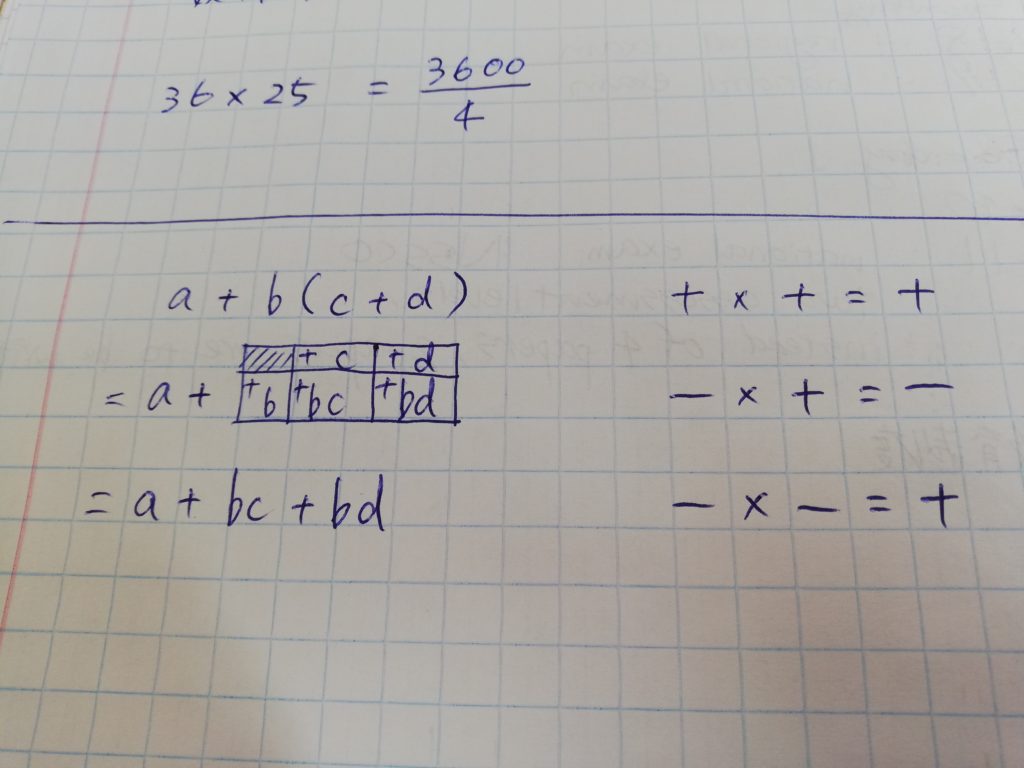
笑いの感覚
「子ども達の学習のためには、よい人間関係が大切です。教師と子どもの関係や、教師同士が助け合う関係も大事です」って話がありました。
「teacher-learner relationship と言っても、ロマンティックな関係ではありません」一同笑…みたいな。。こっちの人のユーモアなんだと思うけど、自分は正直に気持ち悪いなって思っちゃいます。
笑いの感覚②
プラス×プラス=プラス
プラス×マイナス=マイナス
マイナス×マイナス=プラス
の例で、
Goodな人がGoodなことをするとGood
Goodな人がBadなことするとBad
でもBadな人がBadなことすると…Good!!
一同大喜び…みたいな。
こっちの人のユーモアなんだろうと思うけど、数学じゃないじゃんね!
今回のコングレスは評価がテーマになっていました。なので評価が大事ですよ〜という話もたくさん上がっていて。私がもっと考えたいのは、算数で身につける能力ってどんなものなんだろうってこと。センスある的な表現でまとめないで、数の感覚、量の感覚、立体の感覚、図で表す感覚…これを身につけさせたい、だからこんな授業にして、こんな評価をして…ってなるんだと思います。
こういうの、本当に大事だと思う。
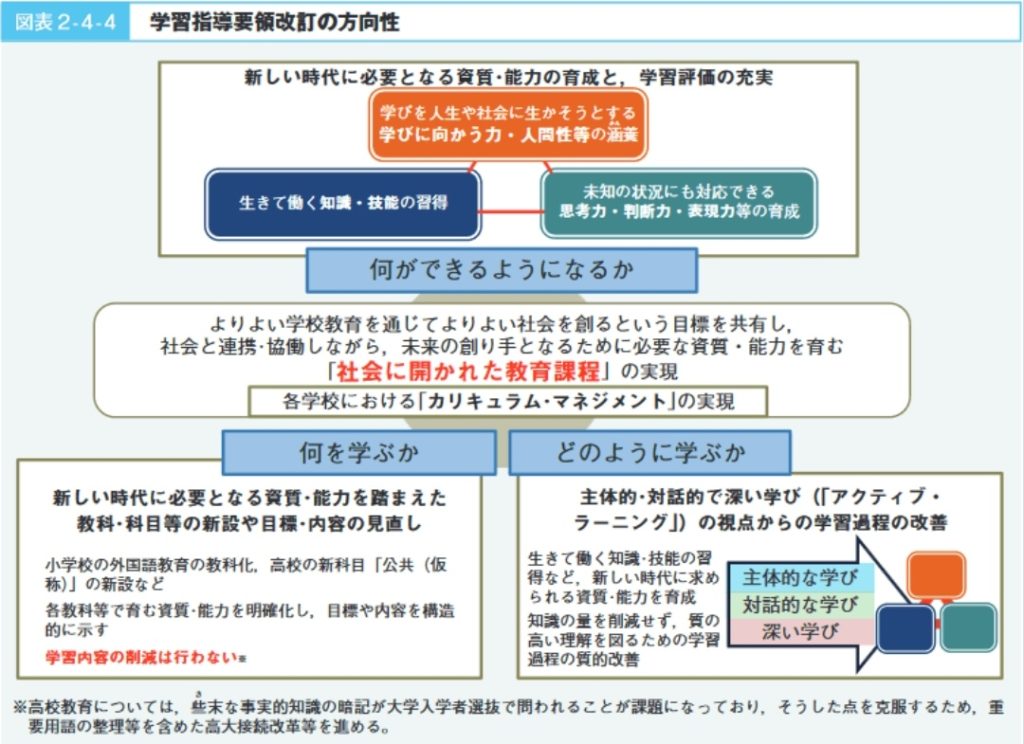
二学期からの活動の中では、どんな力、というのをもう少し考えていきたいと思います。










最近のコメント